相関とは異なる2つの事象の間で、片側の傾向が強くなることによって、もう片側に影響を及ぼす関係性のことです。
ここでは、科学的な相関関係の存在の判断をするために必要な相関係数の求め方や、意味について分かりやすく説明していきます。
目次
相関とは
はじめに相関とは何かについて端的に説明します。
相関の意味・定義
相関とは、2つの事象間に存在する関連性のことを指しています。
ここでいう関連性とは、事象Aの度合いが強い傾向があると、事象Bの度合いが事象Aに比例(反比例)して強く(弱く)なることを意味しています。これらの関係性を、相関関係と呼びます。
後ほど、分かりやすく具体例を混ぜて相関について紐解いて参ります。
相関係数とは
相関分析を行うと、相関係数が求められます。相関係数は一般的に「r」と表記されます。
相関係数とは、2つの事象間に存在する関連性の強弱の度合いを示す数値のことです。
以下に、相関係数を指標とした関係性の判断基準を表にまとめました。相関係数は、-1 < r < 1の範囲で算出され、-1や1に近づく程に強い相関関係があるといわれています。そして、相関係数が+の場合は正の相関関係、−の場合は負の相関関係です。
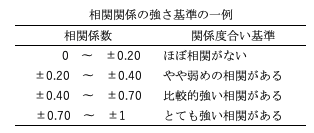
反対に、相関係数が0に近い場合は、事象間に相関関係が存在しない、無相関であるとされます。
相関係数の求め方
相関係数を求める場合に必要な数式は以下の通りです。
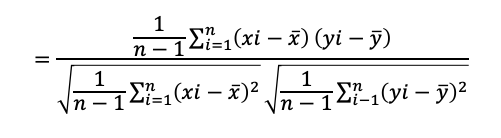
計算方法は
i. まずは括弧を外すために、x(事象A)とy(事象B)の2つのデータ別の平均値を求めます。
ii. xとyの2つの元データ1つ1つを、それぞれの平均値で引き算します。(ここまでで括弧内を全て処理することができました)
iii. (分母)引き算した数値を全て2乗し、xとyで求められた数値を、それぞれ全て足し合わせます。
iv. (分母)xとyそれぞれを足し合わせた数値をデータ数-1で割りましょう。(分母の処理ができました)
v. (分子) ii.で引き算した数値をデータごとにxとyで掛け算し、求められた数値を足し合わせてデータ数-1で割りましょう。(分子の処理ができました)
vi. 最後に、分母のxとyを掛け算し、分子を割ることで相関係数が求められます。
相関関係の具体例
それでは、これまでの話に挙がっていた正の相関、負の相関、無相関について、「学習成績」「学習時間」「アルバイト時間」「体重」の4つの事象を用いて具体的に説明していきます。
正の相関
正の相関とは、事象Aの傾向が高くなることに比例して、事象Bも高くなる関係を指します。
散布図で表すと以下のように、右上がりにデータが配置される形になります。
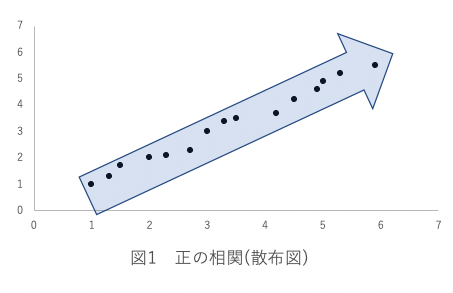
例えば、学習時間(事象A)と学業成績(事象B)の関係性を明らかにするために相関分析を実施した際に、r = .70の結果を得たとします。
この結果から、学習時間と学業成績の間には、比較的強めの正の相関関係があり、学習時間(学業成績)が高ければ高い程、学業成績(学習時間)も比例して高くなると説明することができます。
負の相関
負の相関とは、事象Aの傾向が高くなることに反比例して、事象Bは低くなる関係を指します。
散布図で表すと以下のように、右下がりにデータが配置される形になります。
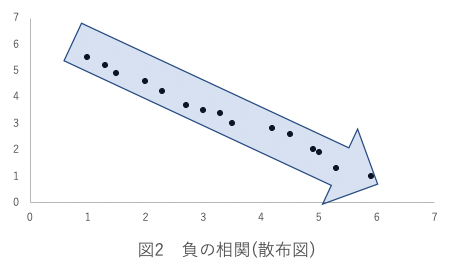
例えば、アルバイト時間(事象A)と学業成績(事象B)の関係性を明らかにするために相関分析を実施した際に、r = -.60の結果を得たとします。
この結果から、アルバイト時間と学業成績の間には、強めの負の相関関係があり、アルバイト時間(学業成績)が高ければ高い程、学業成績(アルバイト時間)は反比例して低くなると説明することができます。
無相関
無相関とは、事象Aの傾向が高く(低く)なったとしても、事象Bには何も影響を及ぼさない関係を指します。
散布図で表しても以下のように、意味のないバラついたデータとなります。
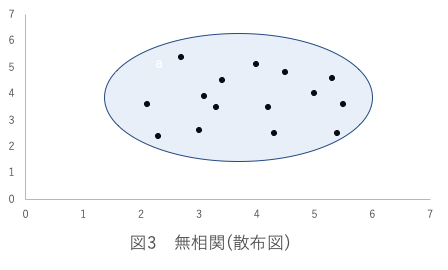
例えば、体重(事象A)と学業成績(事象B)の関係性を明らかにするために相関分析を実施した際に、r = .07の結果を得たとします。
この結果から、体重と学業成績の間には相関関係がないことが示され、どちらのデータが高く(低く)なったとしても、もう片側のデータを高く(低く)する関係性を持たない、無相関であると説明することができます。
相関分析の方法
ここまで具体例を混ぜて相関について説明してきました。
ここからは、実際に相関分析をしようとなった際に、皆さまに知っておいていただきたい補足情報や、簡単に相関分析処理をすることができるオススメのツールを紹介していきます。
相関分析が有効な場合
この記事内で触れた相関分析(ピアソンの積率相関)では、2つの事象データが正規分布していることと、間隔尺度・比率尺度であることが有効となる必要条件として挙げられます。
相関分析ができるツール
実際に相関分析を試してみたいという人にオススメのツールを2つ紹介します。
SPSS
はIBM社が販売している統計解析ソフトで、学生の方は一年間1万6000円程度で契約することができます。
このツールは、一部の大学では学内に限り、学生は無償で使用できるようになっていることもあり、一番スタンダードな統計解析ソフトです。
HAD
はExcelを用いたプログラムで、関西学院大学社会学部の清水裕士教授が開発された誰でも無償で使用することができる統計解析ツールです。
無償でありながらも、SPSSと同様に正確な統計解析を行うことができ、利便性がとても高いため、愛用している人も多いのではないでしょうか。
相関分析を行う際の注意点
相関分析は事象間の関連性を確認する便利な分析法ですが、特に注意すべき点が2つあります。
外れ値の存在

外れ値とは、上の図にあるように、本来であれば正の相関関係を示す綺麗な散布図となるデータの中で、異常ともとれる突飛なデータが紛れ込んだことにより、相関係数に大きな影響を及ぼします。
これでは、折角良いデータを収集できたとしても台無しとなってしまいます。相関分析を行う際には、事前に記述分析をするか散布図を書くことで外れ値が混ざっていないか、必ず確認してください。
偽物の相関関係
相関係数で正(負)の相関関係が認められたとしても、必ずしもそこにデータ間の関連性があるとは断言できません。
例えば、ある調査でアイスクリームの1日の売上高と犯罪発生率に正の相関関係があることが判明したとしましょう。この結果から、アイスの中に人間に犯罪衝動を持たせる物質が混ざっている可能性を危惧し、アイスクリームを全面廃止した所で、犯罪発生率に変化は生じません。
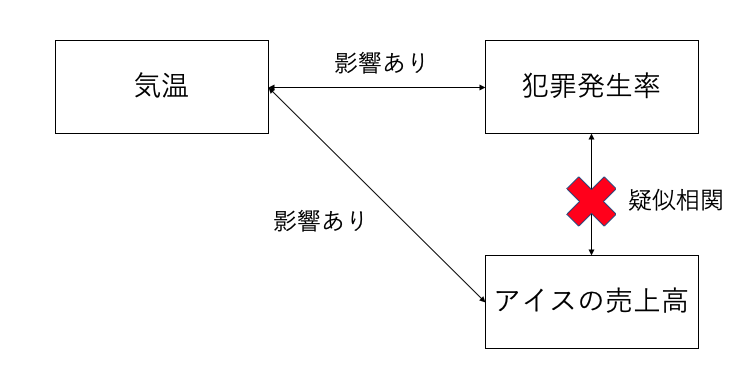
上の図にある通り、アイスクリームの売上高が上がった要因は気温が暑くなったことにありました。それと同時に、気温が暑くなったことによって腹が立って犯罪に走る人が増えていました。
この様に、同様に気温と正の相関関係を持つ関連性のない事象が、偶然、正の相関関係を持っているように見せかける疑似相関に騙されてしまわないようにしましょう。
相関についてわかりやすく学べる本
相関をはじめとする心理統計について学びを深めたいという方へおすすめの本を紹介します。
正しい分析法を理解することで学術論文も読みやすくなる
皆さまは、心理学が文系分野・理系分野どちらに属しているイメージを持っていますでしょうか。
文学部に心理学が所属していることもあり、心理学=文系領域のイメージが強いと思いますが、心理学と統計学の関係性は根強く一概に文系と判断することは難しい学術分野です。
心理学の先行研究を読み漁ろうと論文を読んでみると、研究後にデータを統計学処理して説明しているものが多くあると思います。
そんな時に、相関をはじめとする統計学を勉強していると統計図を見るだけで内容を理解し、文章もなめらかに読み解くことができ、論文により多く触れることができるはずです。
参考文献
白井祐浩著「統計嫌いのための心理統計の本」(2017) 創元社
山田剛史・村井潤一郎著「よくわかる心理統計」(2004) ミネルヴァ書房